十大经典算法导图

图片名词解释:
- n: 数据规模
- k:“桶”的个数
- In-place: 占用常数内存,不占用额外内存
- Out-place: 占用额外内存
冒泡排序
原始人冒泡排序
原理图:
1 | //从小到大,先排好最大的(最后面的) |
进化版冒泡排序
对上述冒泡排序的一种优化, 优化思路:当一次遍历前后数组不产生变化时,说明该数组已经有序,结束排序。
原理图:
1 | // 如果在某次的排序中没有出现交换的情况, |
冒泡动图: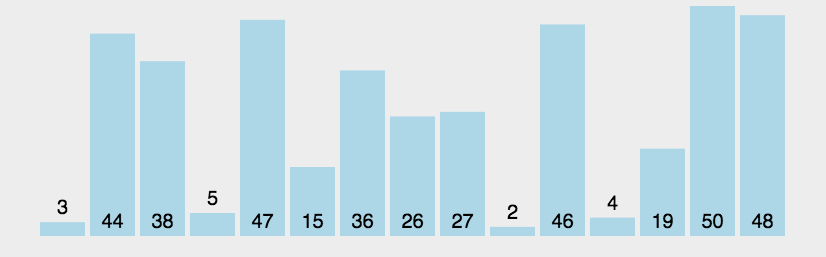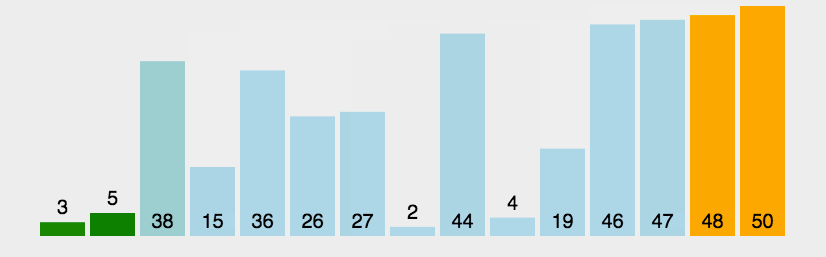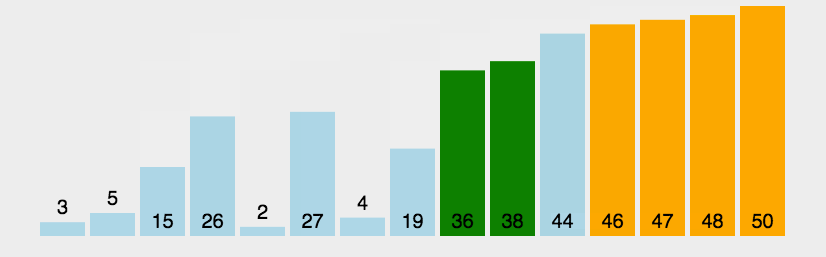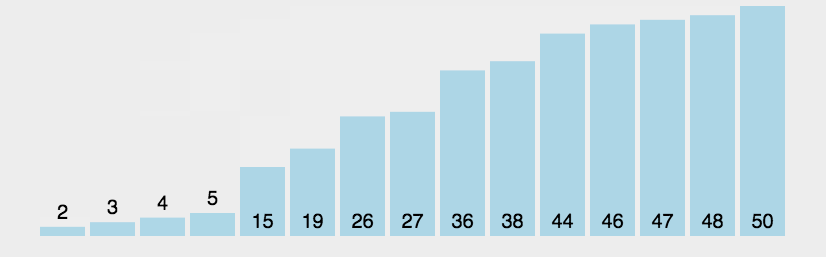
选择排序
实现思路跟冒泡排序差不多, 可以说是冒泡排序的衍生版本;
原理图:

1 | function selectionSort(arr) { |
选择排序动图:
插入排序
最普通的排序算法, 从数组下标1开始每增1项排序一次,越往后遍历次数越多;
打个比方就类比水浒传一百单八将的排名吧,每个好汉来了不知道自己排老几,怎么办,那就和已经排过级别的人比较,然后找到其对应的位置,单八将宋万、杜迁先上的梁山,先默认杜迁第一来的也是单八将最厉害的,然后宋万来了,一比较宋万厉害,那宋万排第一,杜迁排第二,接下来朱贵来了,朱贵没他们两个厉害,那就排第三,再后来林冲来了,林冲比他们三个都厉害,那林冲排第一,宋万第二,杜迁第三,朱贵第四,依次类推。梁山排名其实就是典型的插入排序。
原理图:
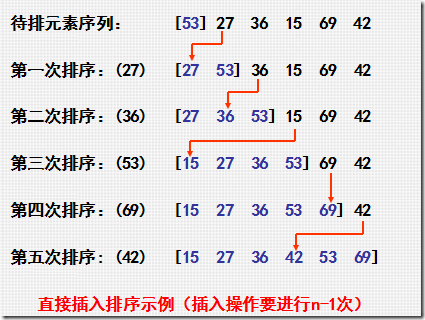
1 | function insertionSort(array) { |
二分插入排序
插入排序的一种优化实现, 通过二分法减少遍历时间。
原理图:
1 | function binaryInsertionSort(array) { |
代码解释:
首先外层循环没什么疑问,就是简单的遍历一遍数组,那么先看while循环,left和right两个变量可以简单的类比上面插入排序中的已排序的首末两个位置,然后选取未排序的第一个值和已排序的中间位置的值进行比较,这样的话也就是在最坏的情况下每层循环也只是计算了已排序的序列长度的一半的次数,简而言之就是在无限逼近left和right值,找到未排序第一个值应该在的位置。
还是以梁山排名为例子,在宋江没有到梁上之前,每个上梁上的人跟已经排过名的从大往小进行比较,然后找到自己的位置,在老大宋江来之后,后续人慢慢多了,然后宋老大就订了条规矩,就是每个新来的人和已排过名次的位于中间名次的好汉进行比较,胜了往前一位比较,败了往后一位比较,然后找到自己的位置。好了,while循环解释完毕,那么下面又多了一条for循环,这又是什么鬼?
不要着急,待小编与你慢慢道来,看不懂没关系,先看循环体,循环体的意思就是把前一个值给后一个,然后看循环条件是从i-1的位置从后往前依次将前一个元素的值给后一个,先不要管i-1是谁,先问 i 是谁,i 不就是未排序的第一个元素么,不就是我们拿来对已进行排序的元素么,简而言之不就是新上梁山的好汉么,那么从left值开始到 i-1 的位置依次将前一个元素的值给后一个无非就是空出 left 的位置,left 的位置不就是新上梁上好汉的位置!
二分插入排序动图: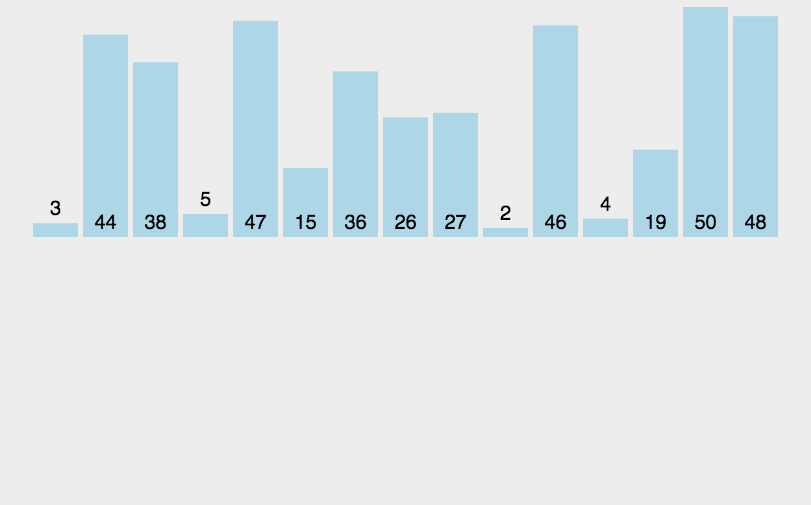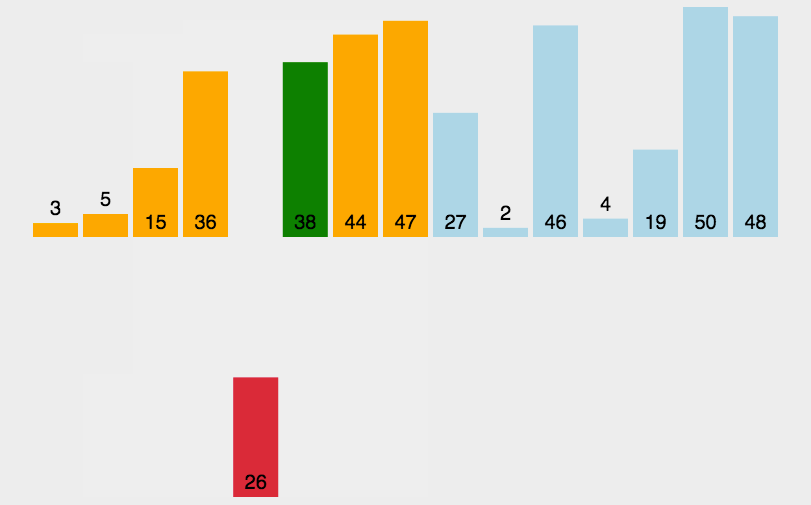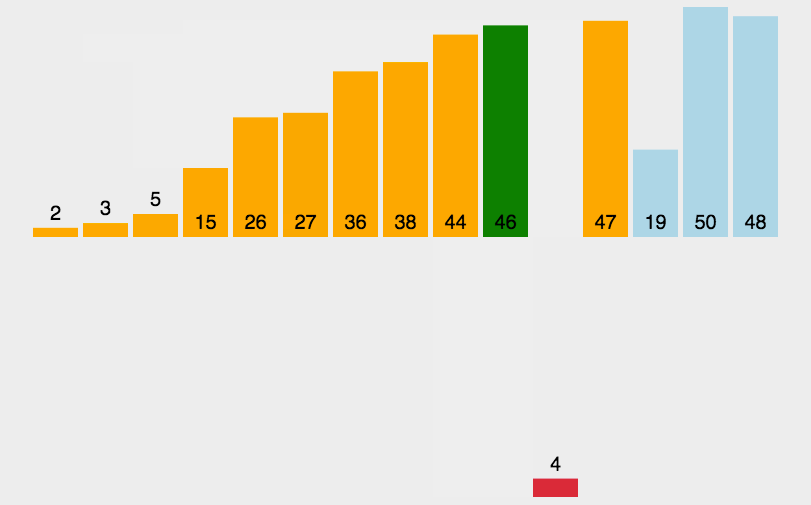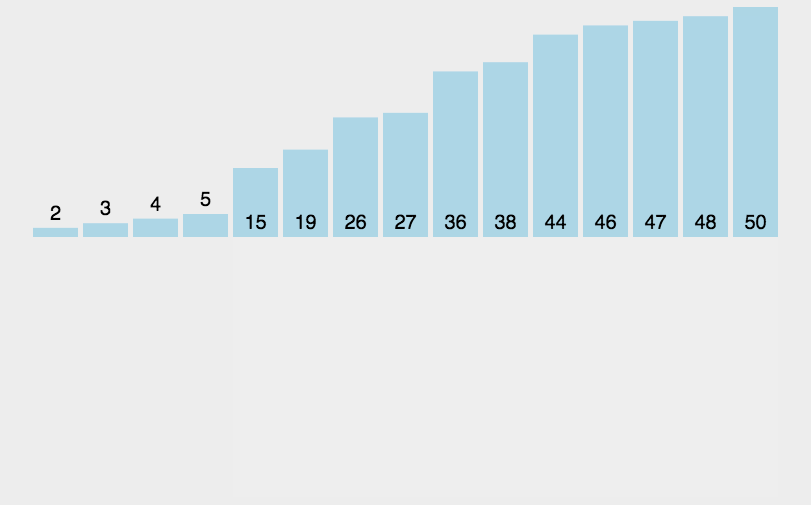
希尔排序
也称为缩小增量排序,同时该算法是冲破O(n2)的第一批算法之一
原理:
先将整个待排序记录序列分割成若干个子序列,在序列内分别进行直接插入排序,待整个序列基本有序时,再对全体记录进行一次直接插入排序;
像比赛一样,1-6一组,2-7一组,每差5为一组进行比较,之后再每差2为一组进行比较,最后就是两两比较
原理图:
1 | function shellSort(arr) { |
1 | function shellSort2(a) { |
归并排序
原理图:
比如现在有个十万人的司令部,习大大是首长,习大大跟司令说了,把所有的人按年龄排序,司令想了,让我一个人也忙活不过来啊,这怎么办,然后就把任务下达给军长,军长下达给师长,依次类推,排长再把一个排分成两个小队,小队再分成两个小组,最后分成两个人一组或一人一组,接下来就是组员之间进行比较,完了小队与小队比较,排与排之间比较,依次类推,最后军团和军团比较,形成最后的序列。
1 | function mergeSort(arr) { //采用自上而下的递归方法 |
并归排序动图: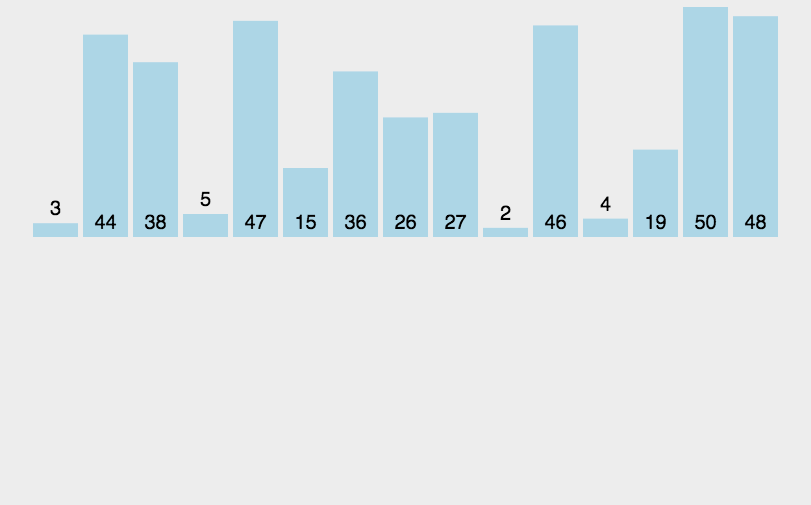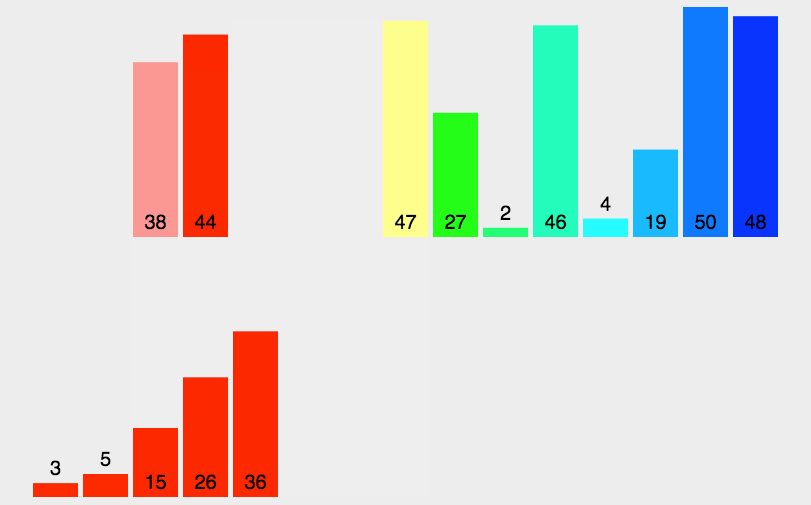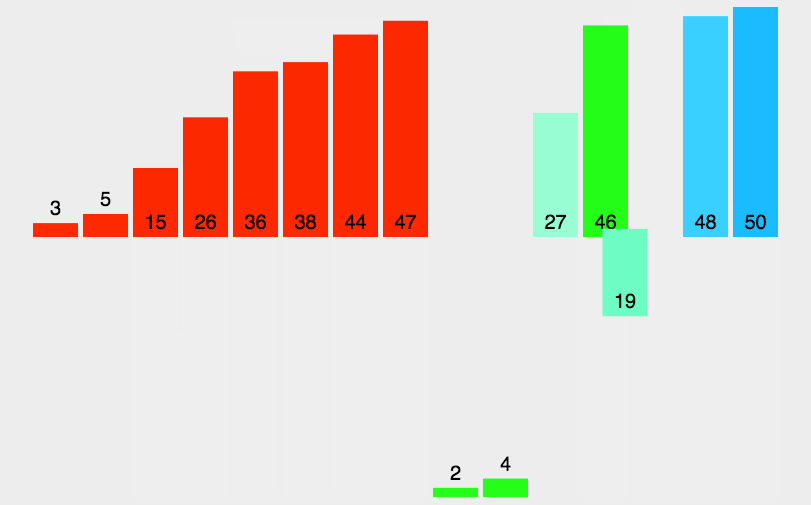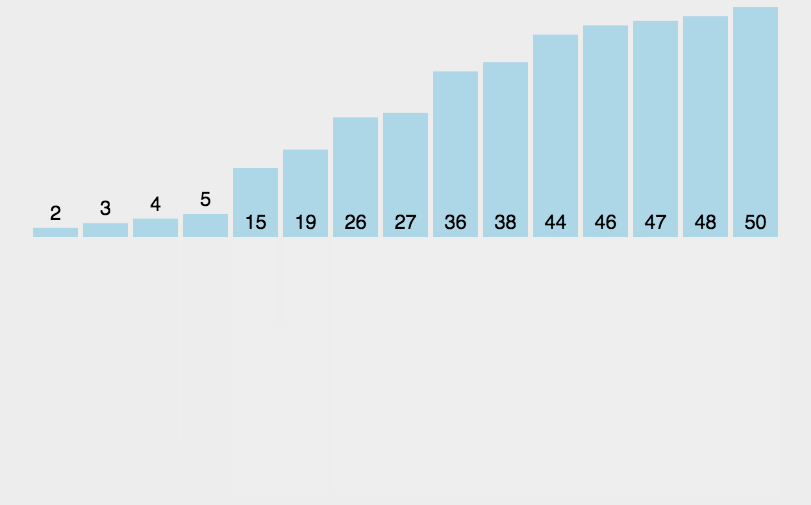
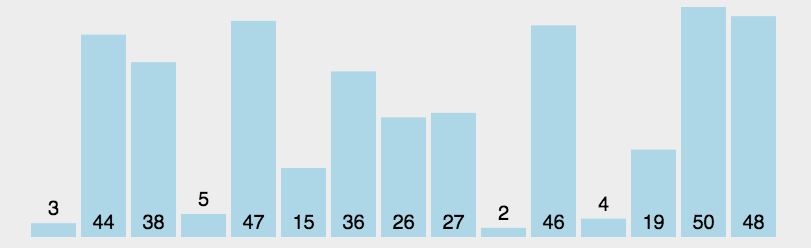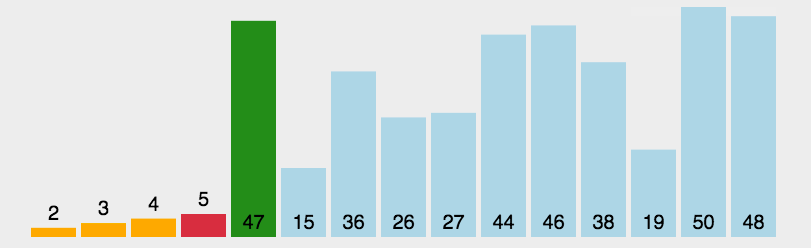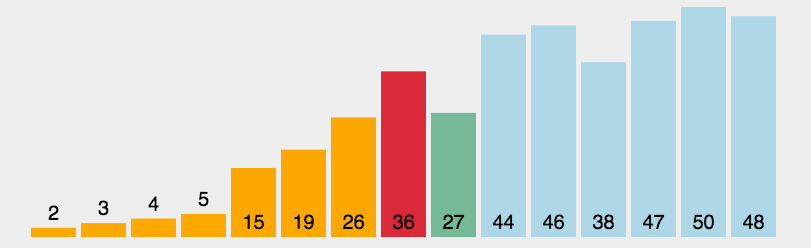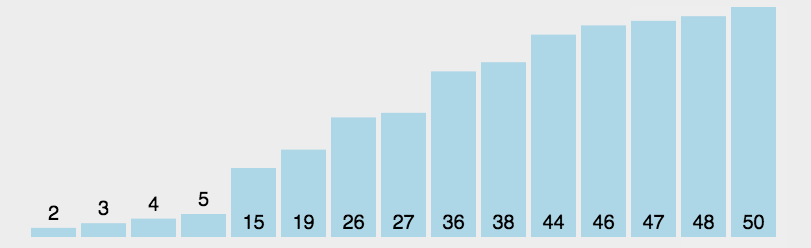
快速排序
快速排序在诸多算法排序中可能不是最好的, 但在JS语言实现中差不多是最快的!
阮一峰老师研究JS实现排序时曾只针对该种排序进行讲解:javascript的快速排序实现。
步骤:
- 在数据集之中,选择一个元素作为”基准”(pivot)。
- 所有小于”基准”的元素,都移到”基准”的左边;所有大于”基准”的元素,都移到”基准”的右边。
- 对”基准”左边和右边的两个子集,不断重复第一步和第二步,直到所有子集只剩下一个元素为止。
原理图:

1 | var quickSort2 = function(arr) { |
快速排序动图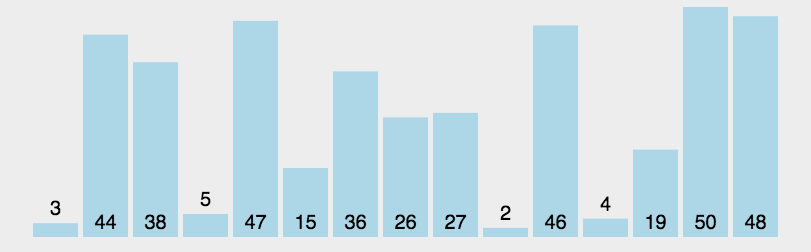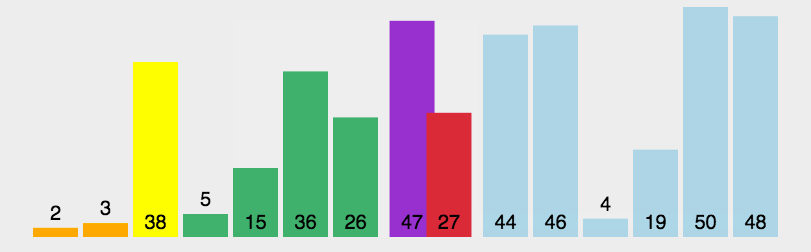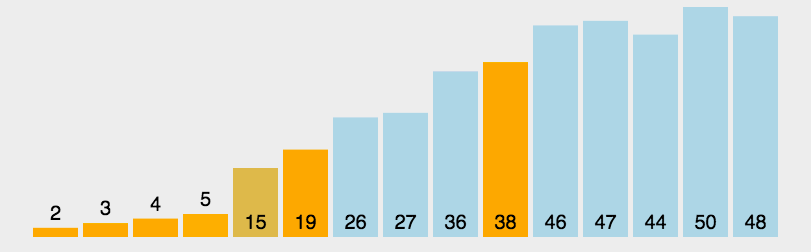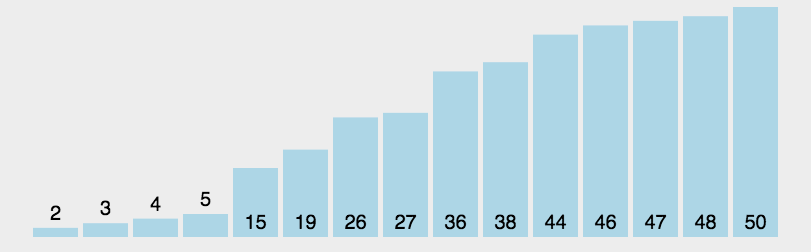
堆排序
因为js模拟二叉树比较麻烦,所以堆排序的优势用js语言无法体现, 相对而言C语言的链表在实现上更能表现堆排序,堆排序或许更适合指针类的计算机语言。
原理图:
1.调整二叉树,形成大根堆(子节点都比父节点小)。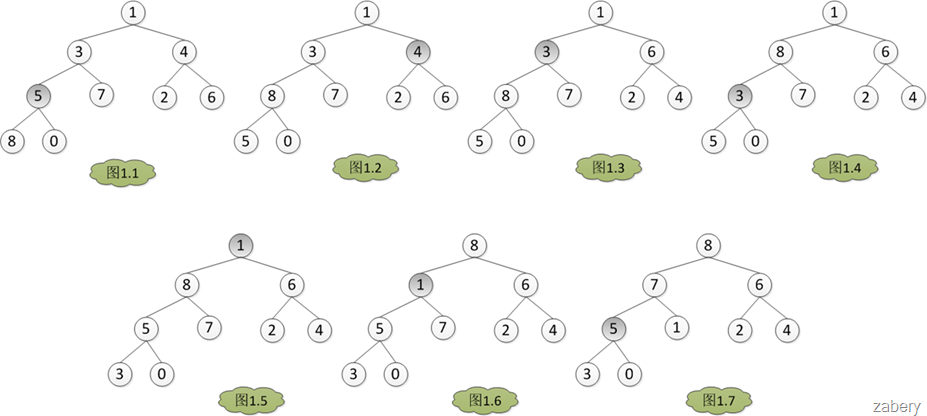
2.交换堆第一元素跟最后元素位置,最后元素弹出堆。然后继续回到1,调整堆。
3.重复2, 当所有节点弹出堆后;弹出的节点值就是有序的了。
1 | function heapSort(array) { |
这种算法有两个难点,一是建堆,而是堆排序。首先明白什么是堆,堆其实可以这么理解,类似金字塔,一层有一个元素,两层有两个元素,三层有四个元素,每层从数组中取元素,从左到右的顺序放到堆相应的位置上,也就是说每一层元素个数为2n-1 ;(n 代表行数),这就完成了建堆。
那么想,堆排序中最后一位不就是2n-m(n代表总行数,m代表差多少位不到完成堆的位数),那该元素的父级是谁,2n-1-m/2,2n-1-m/2是谁?拿总位数除以2就知道了,没错就是数组的中间值,这也是编者为什么从中间值入手的原因了。
而对于 l = 2x +1 与 r = 2x+2 ,不正是每个父级元素对应的子堆么,每一层的堆排序都能够把本层的最大值剔除出来,这样当所有 层循环结束之后,序列也就完成了。
这一点小编觉得和归并排序有点类似,都是细分到最小单元,从最小单元比较,但是同归并排序有两大点不同,一是堆排序并不像归并那么无序,只是一味的平分数组,而堆排序则是按原始序列排出金字塔式的结构,把最大值一层层往上冒,冒到金字塔最顶端的时候把它踢出来,这样达到排序的效果。
堆排序动图:
计数排序
1 | function countingSort(array) { |
C数组的下标对应的数值就是该下标出现的次数
动图: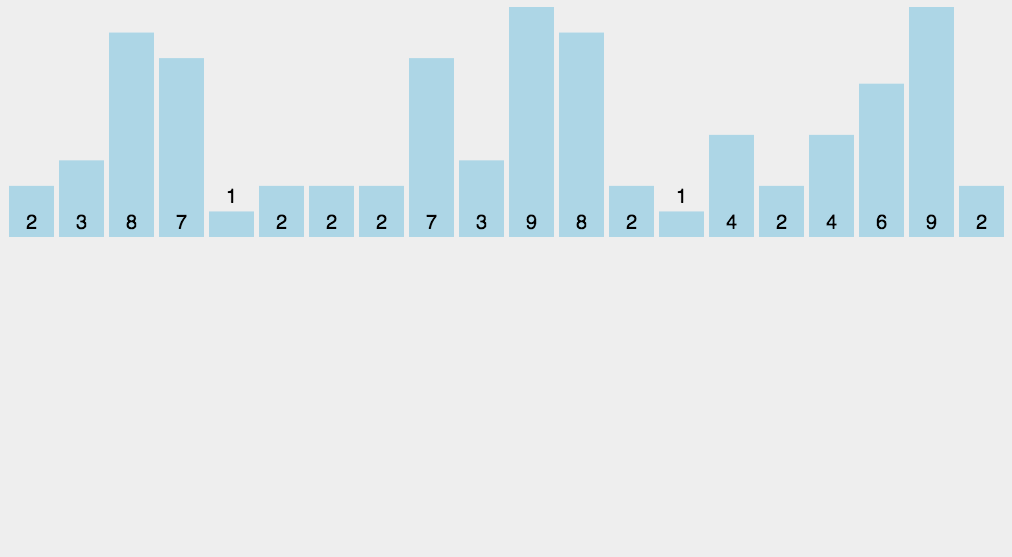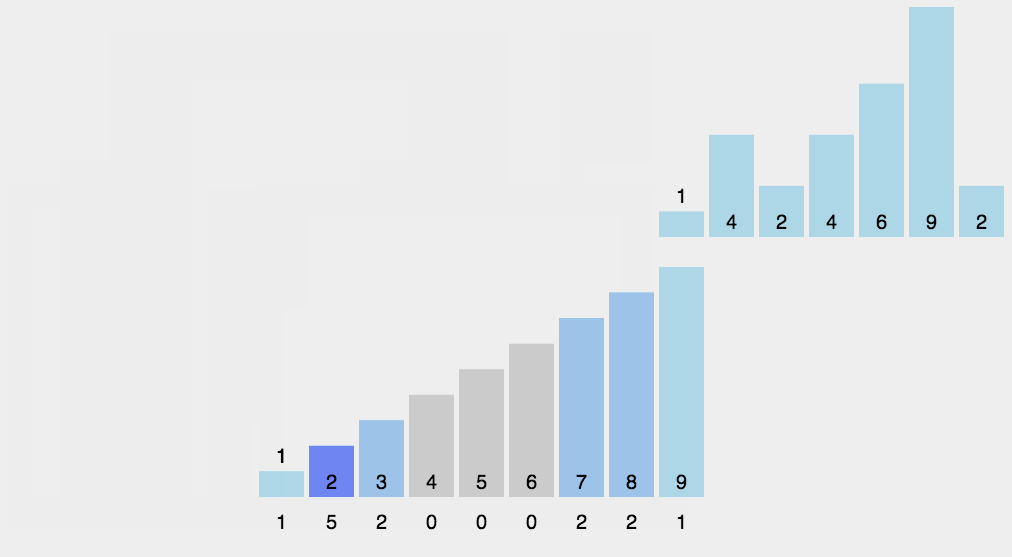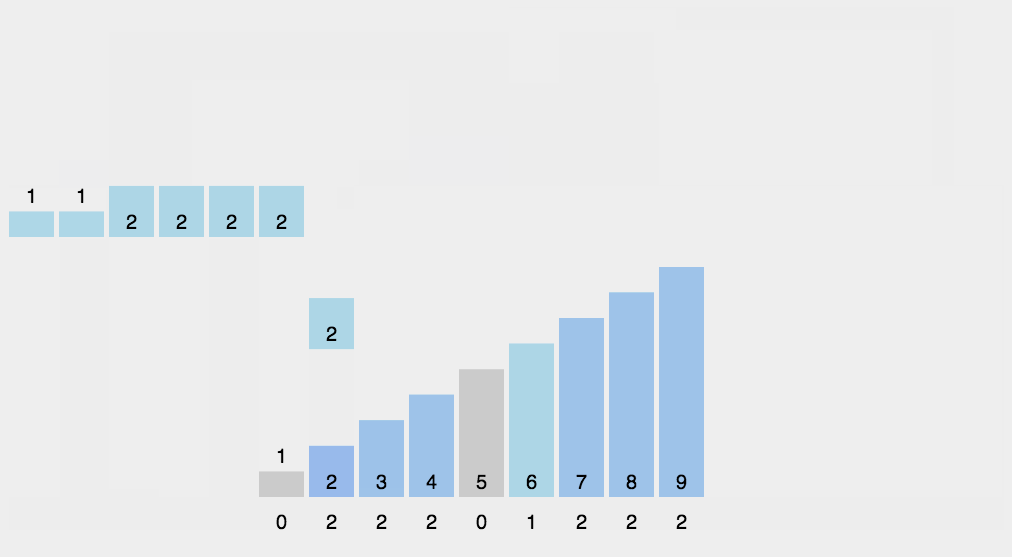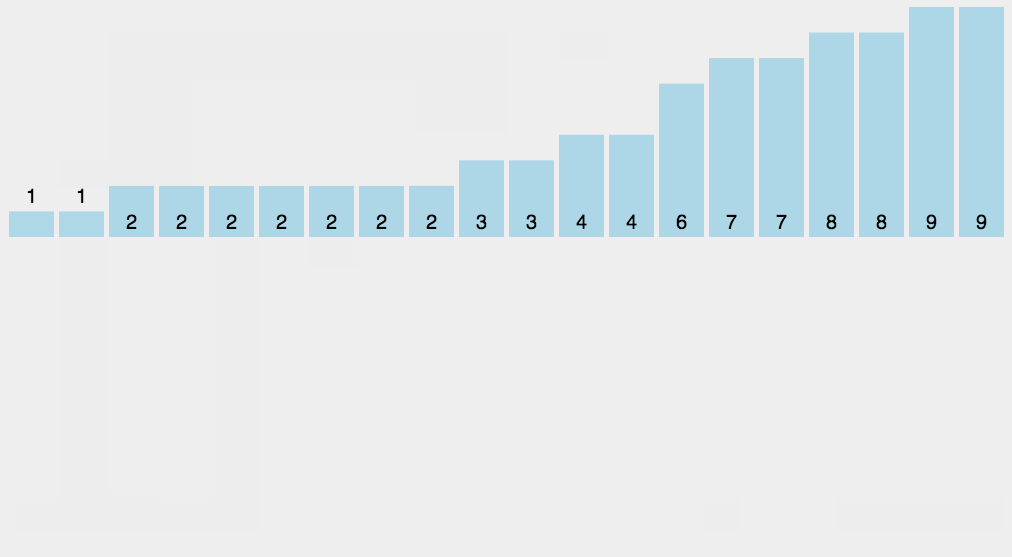
桶排序
一看到这个名字就会觉得奇特,几个意思,我排序还要再准备几个桶不成?还真别说,想用桶排序还得真准备几个桶,但是此桶非彼桶,这个桶是用来装数据用的。其实桶排序和计数排序还有点类似,计数排序是找一个空数组把值作为下标找到其位置,再把出现的次数给存起来,这似乎看似很完美,但也有局限性,不用小编说相信读者也能明白,既然计数是把原数组的值当做下标来看待,那么该值必然是整数,那假如出现小数怎么办?这时候就出现了一种通用版的计数排序——桶排序。
简单例子:
期末考试完了老师要将同学们的分数按照从高到低排序。小哼的班上只有5个同学,这5个同学分别考了5分、3分、5分、2分和8分,哎,考得真是惨不忍睹(满分是10分)。接下来将分数进行从大到小排序,排序后是8 5 5 3 2。
首先我们需要申请一个大小为11的数组int a[11]。OK,现在你已经有了11个变量,编号从a[0]~a[10]。刚开始的时候,我们将a[0]~a[10]都初始化为0,表示这些分数还都没有人得过。例如a[0]等于0就表示目前还没有人得过0分,同理a[1]等于0就表示目前还没有人得过1分……a[10]等于0就表示目前还没有人得过10分。
下面开始处理每一个人的分数,第一个人的分数是5分,我们就将相对应的a[5]的值在原来的基础增加1,即将a[5]的值从0改为1,表示5分出现过了一次。
第二个人的分数是3分,我们就把相对应的a[3]的值在原来的基础上增加1,即将a[3]的值从0改为1,表示3分出现过了一次。
注意啦!第三个人的分数也是5分,所以a[5]的值需要在此基础上再增加1,即将a[5]的值从1改为2,表示5分出现过了两次。
按照刚才的方法处理第四个和第五个人的分数。最终结果就出来了
你发现没有,a[0]~a[10]中的数值其实就是0分到10分每个分数出现的次数。接下来,我们只需要将出现过的分数打印出来就可以了,出现几次就打印几次,具体如下。
桶排序与计数排序很相似,不过现在的桶不单计数,是实实在在地放入元素。举个例子,学校要对所有老师按年龄进行排序,这么多老师很难操作,那么先让他们按年龄段进行分组,20-30岁的一组,30-40岁一组,50-60岁一组,然后组内再排序。这样效率就大大提高了。桶排序也是于这种思想。
操作步骤:
- 确认范围,亦即求取原数组的最大值与最小值。
- 确认需要多少个桶(这个通常作为参数传入,不能大于原数组长度),然后最大值减最小值,除以桶的数量,但得每个桶最多能放多个元素,我们称这个数为桶的最大容量。
- 遍历原数组的所有元素,除以这个最大容量,就能得到它要放入的桶的编号了。在放入时可以使用插入排序,也可以在合并时才使用快速排序。
- 对所有桶进行遍历,如果桶内的元素已经排好序,直接一个个取出来,放到结果数组就行了。
1 | var arr = [2,5,3,0,2,8,0,3,4,3] |
基数排序
基数排序按照对位数分组的顺序的不同,可以分为LSD(Least significant digit)基数排序和MSD(Most significant digit)基数排序。
LSD基数排序
LSD基数排序,是按照从低位到高位的顺序进行分组排序。MSD基数排序,是按照从高位到低位的顺序进行分组排序
对于序列中的每个整数的每一位都可以看成是一个桶,而该位上的数字就可以认为是这个桶的键值。比如下面数组
[170, 45, 75, 90, 802, 2, 24, 66]
首先我们要确认最大值,一个for循环得最大数,因为最大数的位数最长。
然后,建立10个桶,亦即10个数组。
然后再遍历所有元素,取其个位数,个位数是什么就放进对应编号的数组,1放进1号桶。1
2
3
4
5
6
7
80号桶: 170,90
1号桶: 无
2号桶: 802,2
3号桶: 无
4号桶: 24
5号桶: 45, 75
6号桶: 66
7-9号桶: 无
然后再依次将元素从桶里最出来,覆盖原数组,或放到一个新数组,我们把这个经过第一次排序的数组叫sorted。
sorted = [170,90,802,2,24,45,75,66]
然后我们再一次遍历sorted数组的元素,这次取十位的值。这时要注意,2不存在十位,那么默认为0
1 | 0号桶: 2,802 |
再全部取出来
sorted = [2,802,24,45,66,170,75,90]
开始百位上的入桶操作,没有百位就默认为0:1
2
3
4
50号桶: 2,24,45,66,75,90
1号桶: 170
2-7号桶:无
8号桶: 802
9号桶: 无
再全部取出来
sorted = [2,24,45,66,75,90,170,802]
没有千位数,那么循环结束,返回结果桶sorted
从程序描述如下:
1 | function radixSort(array) { |
字符串使用基数排序实现字典排序
此外,基数排序不局限于数字,可以稍作变换,就能应用于字符串的字典排序中。我们先来一个简单的例子,只对都是小写字母的字符串数组进行排序。
小写字母一共26个,考虑到长度不一样的情况,我们需要对够短的字符串进行补充,这时补上什么好呢?我们不能直接上0,而是补空白。然后根据字母与数字的对应关系,弄27个桶,空字符串对应0,a对应1,b对应2…. 字典排序是从左边开始比较, 因此我们需要用到MST基数排序。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76var character = {};
"abcdefghijklmnopqrstuvwxyz".split("").forEach(function(el, i) {
character[el] = i + 1;
});
function toNum(c, length) {
var arr = [];
arr.c = c;
for (var i = 0; i < length; i++) {
arr[i] = character[c[i]] || 0;
}
return arr;
}
function getBucketNumer(arr, i) {
return arr[i];
}
function radixSort(array) {
var len = array.length;
var loopTimes = 0;
//求出最长的字符串,并得它的长度,那也是最高位
for (let i = 0; i < len; i++) {
let el = array[i];
var charLen = el.length;
if (charLen > loopTimes) {
loopTimes = charLen;
}
}
//将字符串转换为数字数组
var nums = [];
for (let i = 0; i < len; i++) {
nums.push(toNum(array[i], loopTimes));
}
//开始多关键字排序
msdRadixSort(nums, len, 0, loopTimes);
//变回字符串
for (let i = 0; i < len; i++) {
array[i] = nums[i].c;
}
return array;
}
function msdRadixSort(array, len, radix, radixs) {
var buckets = [];
for (var i = 0; i <= 26; i++) {
buckets[i] = [];
}
//入桶
for (let i = 0; i < len; i++) {
let el = array[i];
let index = getBucketNumer(el, radix);
buckets[index].push(el);
}
//递归子桶
for (let i = 0; i <= 26; i++) {
let el = buckets[i];
//el.c是用来识别是桶还是我们临时创建的数字字符串
if (el.length > 1 && !el.c && radix < radixs) {
msdRadixSort(el, el.length, radix + 1, radixs);
}
}
var k = 0;
//重写原桶
for (let i = 0; i <= 26; i++) {
let bucket = buckets[i];
for (let j = 0; j < bucket.length; j++) {
array[k++] = bucket[j];
}
bucket.length = 0;
}
}
var array = ["ac", "ee", "ef", "b", "z", "f", "ep", "gaaa", "azh", "az", "r"];
var a = radixSort(array);
console.log(a);
基数排序动图

基数排序 vs 计数排序 vs 桶排序
这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
- 基数排序:根据键值的每位数字来分配桶
- 计数排序:每个桶只存储单一键值
- 桶排序:每个桶存储一定范围的数值
参考来源:
- https://www.cnblogs.com/liyongshuai/p/7197962.html
- https://www.cnblogs.com/wteam-xq/p/4752610.html
- https://segmentfault.com/a/1190000012923917#articleHeader2
本作品采用 知识共享署名 2.5 中国大陆许可协议 进行许可,欢迎转载,但转载请注明来自JayMo,并保持转载后文章内容的完整。本人保留所有版权相关权利。
本文永久链接:http://jaymo666.github.io/2018/04/03/js十大排序算法详解/